We are a theoretical group exploring how the principles of thermodynamics apply to a wide range of systems. Our research unveils fundamental mechanisms of nature spanning through physics, chemistry, biology and nanotechnology.
Click on the icons below to learn more about the research areas
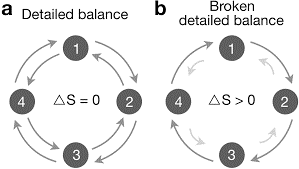
Most of our knowledge on heat machines, molecular machines and chemical networks is based on the assumption that at thermal equilibrium systems keep what is called local detailed balance. Local detailed balance means that, at thermal equilibrium, the rate between any pair transitions is perfectly balanced by the rate of the opposite transition.
Any deviation from this balance requires the system to be out of equilibrium, resulting in the flow of currents in mesoscopic junctions, the transformation of energy in solar cells, or the realization of several biological functions in living systems. Breaking detailed balance is thus an essential thermodynamic resource with several applications.
Non-reciprocal systems have the peculiarity of breaking detailed balance even at equilibrium. This has resulted in many surprising effects: persistent heat currents in thermal equilibrium, violations of the Kirchhoff law, photon thermal hall effect and giant magnetoresistance for the heat flux. We recently found that non-reciprocal materials are needed in order to build a heat engine based on Casimir forces. What other exciting effects can be produced by non-reciprocal systems?
We are investigating this question by building a thermodynamic framework to study non-reciprocal systems and discover other peculiar thermodynamic effects. Moreover, by examining the systems that do not comply with the common assumption of local detailed balance, we are exploring uncharted territories and sharpening the theory of thermodynamics.
Some of the questions that we are studying are:
Some of our papers:
Casimir heat engine using non-reciprocal materials
Near field propulsion forces from non-reciprocal media
Gelbwaser-Klimovsky, D., Graham, N., Kardar, M., & Krüger, M., Physical Review Letters 126.17 (2021): 170401. (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.170401)
https://arxiv.org/abs/2012.12768
Other groups papers:
Persistent heat currents in thermal equilibrium
Persistent directional current at equilibrium in non-reciprocal many-body near field electromagnetic heat transfer
Zhu, L., and Fan S. Physical review letters 117.13 (2016): 134303. (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.117.134303)
https://arxiv.org/abs/1602.08454
Excellent reviews on non-reciprocity:
Electromagnetic non-reciprocity
Caloz, C., Alu, A., Tretyakov, S., Sounas, D., Achouri, K., & Deck-Léger, Z. L. (2018). . Physical Review Applied, 10(4), 047001.(https://journals.aps.org/prapplied/abstract/10.1103/PhysRevApplied.10.047001)
https://arxiv.org/abs/1804.00235
Tutorial on electromagnetic non-reciprocity and its origins
Asadchy, V. S., Mirmoosa, M. S., Díaz-Rubio, A., Fan, S., & Tretyakov, S. A. (2020). Proceedings of the IEEE, 108(10), 1684-1727.
(https://ieeexplore.ieee.org/document/9163137)
https://arxiv.org/abs/2001.04848
Non-equilibrium devices such as thermoelectric devices, solar cells, and heat machines exploit energy/particle currents that flow through a system coupled to multiple baths. Although the fluxes increase as the coupling strengthens in the weak coupling regime, why they decrease to zero for large coupling values remains unknown. This turnover effect has been predicted in several systems such as photosynthetic complexes, thermoelectric devices and chemical networks, without a single counterexample, resulting in a constrained performance due to the limited currents. We also found that this effect limits the performance of heat machines.
The ubiquity of this effect could indicate its universality and a fundamental physical mechanism behind it. In our group, we are studying the turnover effect and unveiling the physical mechanism behind it. For this we use both numerical and analytical methods to analyze the turnover effect and look for common physical behaviors among widely different realizations. Moreover, we are looking for basic design principles that will help avoid or minimize the impact of the turnover effect on microscopic non-equilibrium devices, such as nano-heat machines or thermoelectric devices, and unleash the full potential of these devices.
These are
EXPLORE
The “Turnover Effect” In Heat Engines
Strongly Coupled Quantum Heat Machines
Gelbwaser-Klimovsky, D. & Aspuru-Guzik, A. J. Phys. Chem. Lett. 6, 3477–3482 (2015)
EXPLORE
The “Turnover Effect” In Heat Engines
Strongly Coupled Quantum Heat Machines
Gelbwaser-Klimovsky, D. & Aspuru-Guzik, A. J. Phys. Chem. Lett. 6, 3477–3482 (2015)
The concept of temperature is a central part of equilibrium thermodynamics and statistical mechanics: it is related to several thermodynamics’ laws, it is the key parameter of the equilibrium distribution, and even sets efficiency limitations to work extraction (Carnot bound). No wonder why so many have tried to extend the notion of temperatures to the realm of non-equilibrium systems.
This is achieved by defining an effective temperature, which is generally related to a violation of the fluctuation-dissipation theorem or the use of colored noise. The introduction of an effective temperature has helped reveal the nature of molecular motors in red-blood cell membranes, set bounds to the performance of active Brownian engines, study glasses, and more. Though in some cases the use of an effective temperature provides a good phenomenological description, the models used tend to either use unphysical assumptions such as negative friction or lack a microscopic model that could explain the physical nature of the disequilibrium and its thermodynamic repercussions.
We use the notion of effective temperatures for discovering the limitations that thermodynamics imposes on non-equilibrium systems. To achieve this, we are taking a unique approach and defining effective temperatures from a microscopic physical model. We have already shown that simple properties of these effective temperatures determine the thermodynamic capabilities of a non-equilibrium system. What else can the effective temperature tell us about non-equilibrium systems? For determining this we are studying the concept of effective temperatures in different systems.
Some of the questions we are studying are:
Our papers
Effective temperatures in quantum systems:
Non-equilibrium quantum heat machines
Alicki, R., and Gelbwaser-Klimovsky, D. New Journal of Physics 17.11 (2015): 115012
(https://iopscience.iop.org/article/10.1088/1367-2630/17/11/115012)
https://arxiv.org/abs/1507.01660
Other groups papers
A good review about the effective temperature
he effective temperature
Cugliandolo, Leticia F. Journal of Physics A: Mathematical and Theoretical 44.48 (2011): 483001. (https://iopscience.iop.org/article/10.1088/1751-8113/44/48/483001)
https://arxiv.org/abs/1104.4901
An example of the application of effective temperature to study red-blood-cell
Effective temperature of red-blood-cell membrane fluctuations
Ben-Isaac, E., Park, Y., Popescu, G., Brown, F. L., Gov, N. S., & Shokef, Y. (2011) . Physical review letters, 106(23), 238103. (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.106.238103)
https://arxiv.org/abs/1102.4508
